Koordinat Cartesian
Sistem koordinat cartesian dua dimensi merupakan sistem koordinat yang terdiri dari dua salib sumbu yang saling tegak lurus, biasanya sumbu X dan Y, seperti digambarkan pada gambar di bawah ini :
Jika dilihat dari gambar diatas, koordinat P mempunyai jarak pada sumbu X yang disebut absis sebesar 3 dan mempunyai jarak pada sumbu Y yang disebut ordinat sebesar 5. Sedangkan d merupakan jarak dari pusat sumbu koordinat (O) ke titik P. Nilai d dapat dihitung dengan persamaan :
jika d merupakan jarak antara dua titik, secara umum d dapat dihitung menggunakan persamaan sebagai berikut :
dimana i dan j menunjukkan nama titik.
Dari gambar diatas diperoleh :
B. Geometri
Geometri berasal dari bahasa Yunani geo = bumi, metria = pengukuran secara harafiah berarti pengukuran tentang bumi, adalah cabang dari matematika yang mempelajari hubungan di dalam ruang. Dari pengalaman, atau mungkin secara intuitif, orang dapat mengetahui ruang dari ciri dasarnya, yang diistilahkan sebagai aksioma dalam geometri.
Teorema Phytagoras
Teorema Phytagoras adalah kuadrat panjang sisi miring suatu segitiga siku-siku adalah sama dengan jumlah kuadrat panjang sisi-sisi yang lain.
C. Trigonometri
Trigonometri berasal dari bahasa yunani trigonon = tiga sudut dan metro = mengukur adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometri seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidak setujuan tentang apa hubungannya, bagi beberapa orang, trigonometri adalah bagian dari geometri.
Hubungan Fungsi Trigonometri
Penjumlahan
Rumus Sudut Rangkap Dua
Rumus Sudut Rangkap Tiga
Rumus Setengah Sudut
Hukum Sinus
Hukum sinus ialah pernyataan tentang segitiga yang berubah-ubah di udara. Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C.
Rumus ini berguna menghitung sisi yang tersisa dari segitiga jika 2 sudut dan 1 sisinya diketahui.
Hukum Cosinus
Hukum kosinus, atau disebut juga aturan kosinus, dalam trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu segitiga, yaitu antara panjang sisi-sisi.
Aturan kosinus menyatakan bahwa segitiga dan kosinus dari salah satu sudut dalam segitiga tersebut.
Contoh Soal dan Pembahasan Dari Materi Titik dan Baris, Geometri, dan Trigonometri
Titik dan Garis
Soal :
1. Carilah 5 titik yang dilalui garis 3x - 2y = 8. Gambarkan pada sistem koordinat Cartesian
2. Buatlah fungsi garis y = f(x) yang melalui titik (1,0) dan (−3,3) dan carilah nilai kemiringannya (slope)
3. Di titik mana kemungkinan terjadinya tabrakan antara mobil yang bergerak pada jalur garis no. 2 dan pada jalur garis –x +3y = −6
2. Buatlah fungsi garis y = f(x) yang melalui titik (1,0) dan (−3,3) dan carilah nilai kemiringannya (slope)
3. Di titik mana kemungkinan terjadinya tabrakan antara mobil yang bergerak pada jalur garis no. 2 dan pada jalur garis –x +3y = −6
Penyelesaian
1. Lima titik yang dilalui garis 3x-2y = 8
Jadi kelima titik tersebut adalah :(0,-4), (1,-21/2), (2,-1), (3,1/2), (4,2)
2. Titik Pusatnya
3. Gambar lingkaran tersebut pada sistem koordinat Cartesian
Gambar kordinat Cartesian
2. Fungsi garis y = f(x) yang melalui titik (1,0) dan (−3,3) dan nilai kemiringannya (slope)
Geometri
Soal dan Penyelesaian
1. Nilai m pada segitiga siku-siku menurut teorema phytagoras
Penyelesaian
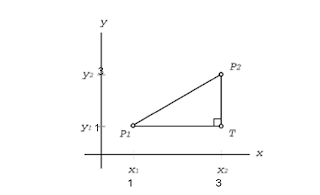
2. Perhatikan gambar di bawah ini. Jika P1 (1,1), P1 (3,3) Maka
a. Kordinat Titik T = (3,1)
b. Jarak P1-P2
c. Jarak P1-T = 2
d. Jarak P2-T = 2
3. Diberikan persamaan lingkaran x2 + (1 + y2) = 9
Tentukan
1. Jari-jari lingkaran (radius)2. Titik Pusatnya
3. Gambar lingkaran tersebut pada sistem koordinat Cartesian
Penyelesaian
a. Jari-jari lingkaran (radius)
b. Titik pusat (h,k) = (0,-1)
c. Gambar lingkaran tersebut pada sistem kordinat kartesian
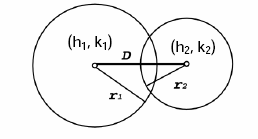
4. Berikan aturan titik pusat dan jari-jari dua lingkaran berikut agar dua mobil yang bergerak pada setiap jalur lingkaran tidak akan pernah terjadi tabrakan.
Penyelesaian
Soal dan Penyelesaian
2. Lengkapi tabel fungsi trigonometri dibawah ini
Tabel fungsi trigonometri setelah dilengkapi :
3. Gambarkan grafik fungsi trigonometri berikut ini :
Penyelesaian
a. y = 2 sin(x), dengan x didalam radian
b. y = cos(2x), dengan x dalam derajat
4. Identitas Trigonometri



































Tidak ada komentar:
Posting Komentar